핸즈온 머신러닝 챕터9 - 비지도 학습
Updated:
핸즈온 머신러닝 챕터9 비지도 학습에서 군집과 관련한 내용을 요약한다.
9.1 군집(clustering)
군집(clustering) : 유사한 데이터들을 서로 묶어주는 데이터 마이닝 기법
클러스터(cluster) : 비슷한 특징을 갖는 데이터 집단
클러스터링은 대표적인 비지도학습이다. 지도학습은 정답이 있는 데이터셋을 이용한다. 여기서 정답은 보통 레이블(label)이란 이름으로 부른다. 레이블은 필요나 상황에 따라 ‘y값, 함수값, 출력, 종속변수’ 등의 이름으로 불리기도 한다.
군집과 유사한 개념으로 분류(classification)가 있다. 둘 다 카테고리를 나눈다는 개념은 비슷하다. 그러나 분류는 지도학습, 클러스터링은 비지도 학습이다. 다음 그림에서 그 차이를 확인할 수 있다.

iris 데이터셋에서 petal length, petal with 특성만을 추출하여 평면상에 나타낸 것이다. 왼쪽(분류, 지도학습)에서는 각 점들이 어떤 꽃인지 레이블이 표시되어있다. 그러나 오른쪽(군집, 비지도학습)에는 각 샘플의 특성만 알 수 있고 어떤 꽃인지는 알 수 없다.
9.1.1 k-평균 알고리즘
주어진 데이터를 k개의 클러스터로 묶는 알고리즘을 말한다. 작동 방식은 다음과 같다.
(1) 초기화 : 주어진 데이터셋에서 무작위로 k개의 샘플을 뽑아 센트로이드(centroid)로 지정한다.
(2) 거리 계산 : 모든 샘플에 대해 각 센트로이드와의 거리를 계산한다.
(3) 클러스터 할당 : 각 샘플들은 가장 가까운 거리의 센트로이드와 하나의 클러스터로 묶인다.
(4) 센트로이드 업데이트 : 모든 샘플들의 클러스터가 정해지면, 각 클러스터에 속한 샘플들의 평균값을 성분으로 갖는 새로운 센트로이드를 지정한다.
(5) 센트로이드가 더이상 바뀌지 않을 때까지 (2)~(4)를 반복한다.
k-평균 알고리즘을 그림으로 표현하면 다음과 같다.
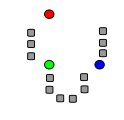 |
처음 센트로이드 k개 (이 경우 k=3)는 데이터들 중에서 무작위로 뽑힌다. (색칠된 동그라미로 표시됨). |
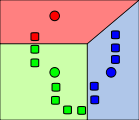 |
데이터셋의 각 샘플들은 가장 가까이 있는 센트로이드를 기준으로 묶인다. 센트로이드 기준으로 분할된 영역은 보로노이 다이어그램 으로 표시된다. |
 |
각 클러스터의 평균으로 센트로이드가 재조정된다. |
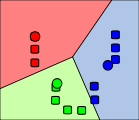 |
수렴할 때까지 2, 3단계 과정을 반복한다. |
9.1.1.1 데이터 생성
예제 데이터를 생성하여 훈련시켜보자.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
blob_centers = np.array(
[[ 0.2, 2.3],
[-1.5 , 2.3],
[-2.8, 1.8],
[-2.8, 2.8],
[-2.8, 1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers,
cluster_std=blob_std, random_state=7)
생성한 2000개의 데이터를 그래프로 나타낸다.
def plot_clusters(X, y=None):
plt.scatter(X[:, 0], X[:, 1], c=y, s=1)
plt.xlabel("$x_1$", fontsize=14)
plt.ylabel("$x_2$", fontsize=14, rotation=0)
plt.figure(figsize=(8, 4))
plot_clusters(X)
plt.show()
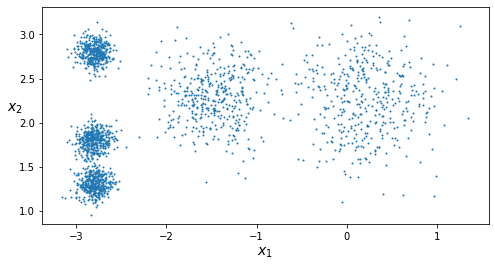
9.1.1.2 훈련 및 예측
사이킷런에서 패키지를 불러와 데이터를 훈련시킨다.
from sklearn.cluster import KMeans
k = 5
kmeans = KMeans(n_clusters=k, random_state=11)
y_pred = kmeans.fit_predict(X)
훈련 과정을 그림으로 표현하면 다음과 같다.

y_pred
array([1, 4, 0, ..., 2, 0, 4], dtype=int32)
2000개의 점이 모두 하나의 클러스터에 할당되었다. 각 클러스터의 센트로이드는 다음과 같다.
kmeans.cluster_centers_
array([[ 0.21087045, 2.25606987],
[-2.80037642, 1.30082566],
[-2.79145317, 2.79524549],
[-1.46280987, 2.28512562],
[-2.80389616, 1.80117999]])
새로운 샘플에 대한 예측은 가장 가까운 센트로이드의 클러스터로 할당하는 것이다.
X_new = np.array([[0, 2], [3, 2], [-3, 3], [-3, 2.5]])
kmeans.predict(X_new)
array([0, 0, 2, 2], dtype=int32)
9.1.1.3 다양한 수렴형태
k-평균 알고리즘의 수렴 형태는 한 가지로 정해져있지 않다. 다음 그림을 보자.

이런 상황이 발생하는 이유는 초기 센트로이드가 무작위로 정해지기 때문이다. 개선 방법은 두 가지가 있다.
< 1. 반복 >
가장 간단하게 알고리즘을 여러번 반복하여 안좋은 상황을 피하는 방법이다. 알고리즘의 반복 횟수를 조절하는 파라미터는 n_init이다. 이 파라미터의 기본값은 10으로 설정되어있다. 이 상태에서 훈련을 진행하면 10번의 훈련을 마친 후 가장 좋은 성능의 모델을 선택한다. 성능의 평가 기준은 이너셔(inertia)이다.
이너셔(inertia) : 데이터셋의 각 샘플에 대해 자신이 속한 클러스터의 센트로이드 까지의 거리를 제곱해서 더한 값.
이너셔를 수식으로 표현하면 다음과 같다.
\[J = \sum_{j=1}^{k}\sum_{i \in C_k} ||x_i - \mu _j||^2 \qquad where \quad C_k : \mathrm{cluster} \quad \mu_j : \mathrm{centriod}\]n_init=10인 경우 10번의 훈련 중 이너셔가 가장 작은 모델이 생성된다. 또한 k-평균 알고리즘은 이너셔가 더이상 감소하지 않는 지점에서 종료된다. 코드로 나타내면 다음처럼 쓸 수 있다.
kmeans = KMeans(n_clusters=k, n_init=10 ,random_state=11)
< 2. k-평균++ >
초기 센트로이드를 무작위로 고르지 않고 조금 더 신중하게 고르는 방법이다. 방법은 다음과 같다.
(1) 데이터셋에서 무작위로 하나의 센트로이드 $\mathbf{c}^{(1)}$를 선택한다.
(2) 각 샘플 $\mathbf{x}^{(i)}$에 대해 확률 $D(\mathbf{x}^{(i)})^2 / \sum_{j=1}^{m} D(\mathbf{x}^{(j)})^2$을 계산한다.
(3) 계산한 확률값을 기준으로 다음 센트로이드를 선택한다.
(4) k개의 센트로이드가 선택될 때까지 전 단계를 반복한다.
여기서 $D(\mathbf{x}^{(i)})$는 샘플 $\mathbf{x}^{(i)}$와 가장 가까운 센트로이드까지의 거리이다. 이 알고리즘은 초기 k개의 센트로이드를 고를 때 서로 멀리 떨어진 샘플이 선택될 ‘확률’을 높인다.
사이킷런의 KMeans 클래스는 기본적으로 K-means++ 방식을 택한다. 기존의 K-means 방법을 이용하고 싶다면 다음과 같이 init 파라미터를 random으로 지정하면 된다.
kmeans = KMeans(n_clusters=k, init='random' ,random_state=11)
9.1.1.4 최적의 클러스터 수 k 찾기
k-평균 알고리즘은 적절한 클러스터의 수를 지정하는 것이 관건이다. 다음 그림은 잘못된 k 값으로 훈련된 결과를 보여준다.

적절한 k값을 찾는 방법은 두 가지가 있다.
< 1. 엘보 >
이너셔의 감소폭이 급감하는 지점을 엘보라 부른다.

연속적인 k값을 택하여 훈련을 진행한 뒤 이너셔의 감소율을 계산하여 엘보의 k값을 택한다.
< 2. 실루엣 점수(silhouette score) >
실루엣 점수는 엘보를 찾는것보다 더 많은 계산을 필요로 하지만 조금 더 정확한 결과를 얻을 수 있다.
(1) 실루엣 점수(silhouette score) : 모든 샘플에 대한 실루엣 계수의 평균
(2) 실루엣 계수(silhouette coefficient) $={(b-a) \ / \ max(a,b)}$
실루엣 계수는 각각의 샘플마다 별도로 계산된다. $a$는 같은 클러스터에 속한 다른 샘플들 까지의 평균 거리이다. 즉 클러스터 내부의 평균거리로써 데이터의 응집도를 나타낸다.
$b$는 가장 가까운 외부 클러스터에 속한 샘플들까지의 평균 거리로써 데이터의 분리도를 나타낸다. $a$가 작을수록 하나의 클러스터 안에 데이터들의 밀도가 높으며 $b$가 클수록 클러스터들 사이에 빈 공간이 많다.
실루엣 계수는 $a$와 $b$의 대소관계에 따라 다음과 같은 값을 갖는다.
\[{b-a \over max(a,b)} = \begin{cases} 1 - {a \over b} & \mbox{if} \quad b > a \\ 0 & \mbox{if} \quad b = a \\ {b \over a} - 1 & \mbox{if} \quad b < a \end{cases}\]따라서 실루엣 계수는 -1부터 1 사이의 값이다. 1에 가까울수록 자신의 클러스터와 잘 속해있고 0에 가까울수록 서로 다른 클러스터의 경계에 위치하며 -1에 가까울수록 잘못된 클러스터에 할당되었다는 의미이다.
위의 예제 데이터셋에 대한 실루엣 점수는 사이킷런의 silhouette_score 클래스로 구할 수 있다.
from sklearn.metrics import silhouette_score
silhouette_score(X, kmeans.labels_)
0.655517642572828
k값을 달리하여 실루엣 점수를 구하여 비교해볼 수 있다.

$k=4$일때 실루엣 점수가 가장 높지만 실루엣 점수의 최대값이 가장 이상적인 클러스터링을 보장하지는 않는다.
모든 샘플에 대해 실루엣 계수를 구한 뒤 내림차순으로 정렬하여 다음과 같은 실루엣 다이어그램을 그릴 수 있다.

실루엣 다이어그램은 각각의 클러스터를 나타내는 칼모양의 그래프로 이루어진다. 그래프의 높이는 클러스터에 속한 샘플의 개수를 나타내며 클러스터의 너비는 각 샘플의 실루엣 계수이다. 점선의 위치는 실루엣 점수를 나타낸다. 칼 모양의 그래프가 그려지는 이유는 내림차순으로 정렬했기 때문이다.
$k=4$ 일때 실루엣 점수가 가장 높긴 하나, $k=5$일 때 클러스터의 높이가 가장 균일하며 클러스터별 실루엣 계수들의 편차가 가장 적다. 최적의 k값은 $k=5$로 택한다.
9.1.1.5 k-평균의 한계
k-평균 알고리즘은 다음과 같은 한계점을 가진다.
(1) 최적이 아닌 솔루션을 피하기 위해 알고리즘을 여러번 실행
(2) 클러스터의 개수를 직접 지정
(3) 클러스터가 원형이 아닌 경우 잘 작동하지 않음.

위 그림은 타원형 클러스터에 대해 k-평균이 어떻게 작동하는지 보여준다.
9.1.2 k평균 알고리즘의 적용 예시
9.1.2.1 이미지 분할(image segmentation)
이미지 분할의 예시 중 하나인 색상 분할(color segmentation) 에 대해 알아보자.
우선 다음과 같은 800x533 크기의 무당벌레 사진을 맷플롯립의 imread() 함수를 통해 로드한다.

from matplotlib.image import imread
image = imread('./img/chap9_ladybug.png')
image.shape
(533, 800, 3)
이 이미지는 3차원 list로 표현된다. 가로 800, 세로 533 총 42만개 정도의 픽셀로 이루어져 있으며 각각의 픽셀은 하나의 벡터 $(R,G,B)$ 로 나타낸다. 이 $(R,G,B)$는 해당 픽셀의 색상을 의미한다.
print(image[0])
print('첫 번째 성분의 길이 :' ,len(image[0]))
print('전체 리스트의 길이 :', len(image))
[[0.09803922 0.11372549 0.00784314]
[0.09411765 0.10980392 0.00392157]
[0.09411765 0.11372549 0. ]
...
[0.22352941 0.4117647 0.08235294]
[0.21960784 0.40392157 0.08627451]
[0.20392157 0.3882353 0.07450981]]
첫 번째 성분의 길이 : 800
전체 리스트의 길이 : 533
image는 800개의 $(R,G,B)$ 벡터(1차원 리스트)로 이루어진 2차원 list가 533개 들어있는 3차원 list이다.
해당 이미지를 42만개의 벡터로 이루어진 2D 리스트로 바꾼 다음 학습을 진행한다.
X = image.reshape(-1, 3)
kmeans = KMeans(n_clusters=8, random_state=42).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_img = segmented_img.reshape(image.shape)
print(X)
print('전체 픽셀 수 :', len(X))
[[0.09803922 0.11372549 0.00784314]
[0.09411765 0.10980392 0.00392157]
[0.09411765 0.11372549 0. ]
...
[0.03921569 0.22745098 0. ]
[0.01960784 0.20392157 0. ]
[0.00784314 0.1882353 0. ]]
전체 픽셀 수 : 426400
클러스터링이 완료됐으면 각 클러스터에 속한 픽셀들의 $(R,G,B)$ 값을 모두 센트로이드의 값으로 치환한다. 그 결과는 다음과 같다.

9.1.2.2 전처리
군집은 차원축소에도 이용할 수 있다. 사이킷런의 digits 데이터를 예로 들면 다음과 같다.
from sklearn.datasets import load_digits
이 데이터는 8x8 크기의 숫자 이미지 1797개를 담고 있다. 각 픽셀에는 흑백의 정도를 나타내는 0~255 사이의 숫자가 들어있다. 따라서 하나의 숫자 이미지는 64차원의 벡터로 표현된다. 차원을 축소하는 방법은 다음과 같다.
(1) 훈련 세트를 50개의 클러스터로 모은다.
(2) 각 이미지를 50개의 센트로이드까지의 거리로 바꾼다.
(3) 바꾼 데이터셋으로 분류 알고리즘을 적용한다.
9.1.2.3 레이블 전파
레이블 전파(label propagation)는 레이블이 없는 데이터에 조금 더 효율적으로 labeling을 하는 방법이다. 클러스터링은 레이블 전파의 유용한 도구이다. 예를 들어 digits 데이터셋에 다음과 같은 labeling이 가능하다.
(1) 데이터셋을 k=50으로 클러스터링 한다.
(2) 각 클러스터에서 센트로이드와 가장 가까운 이미지를 찾는다. 이를 대표(representative) 라 부른다.
(3) representative만 수동으로 labeling 한다.
(4) representative의 레이블을 동일한 클러스터 내의 모든 샘플에 부여한다.
9.1.3 DBSCAN
k-평균이 거리 기반 군집이었다면 DBSCAN은 밀도 기반 군집이다. 다음과 같은 특징을 갖는다.
(1) 임의 모양을 갖는 클러스터도 식별할 수 있음
(2) 이상치에 안정적임
(3) 사전에 클러스터 개수를 지정할 필요 없음
(4) 새로운 샘플에 대한 예측 불가
알고리즘 이해를 위해 필요한 용어는 다음과 같다.
(1) $\epsilon$-이웃($\epsilon$-neigborhood) : 하나의 샘플 중심으로 하고 반지름이 $\epsilon$인 영역
(2) 이웃 관계 : 두 샘플 사이의 거리가 $\epsilon$보다 가까울 때 이웃 관계에 있다고 한다.
(3) core point : ($\epsilon$-이웃 내 샘플 수) $\ge$ (min_samples개) 인 샘플
(4) border point : core point의 이웃이면서 core point가 아닌 샘플
(5) noise point : core도 아니고 border도 아닌 샘플
DBSCAN 알고리즘은 하이퍼 파라미터로 $\epsilon$(eps), min_samples 두개를 갖는다. 작동 방식은 다음과 같다.
(1) 모든 core는 하나의 클러스터를 형성한다.
(2) 이웃 관계에 있는 core들의 클러스터는 하나로 합쳐진다.
알고리즘을 그림으로 표현하면 다음과 같다.

사이킷런에서 제공하는 초승달 모양의 데이터셋으로 DBSCAN을 적용해보자.
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)
plt.scatter(X[:,0], X[:,1])
plt.show()

dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit(X)
dbscan.labels_[:20]
array([ 0, 2, -1, -1, 1, 0, 0, 0, 2, 5, 2, 3, 0, 2, 2, 2, 4,
2, 2, 4])
위 데이터셋은 한 눈에 봐도 2개의 클러스터로 군집해야 한다. 그러나 dbscan 결과 0~5까지 6개의 클러스터가 보인다(-1은 noise를 의미한다). 하이퍼 파라미터를 바꿔 다시 훈련시켜보자.
dbscan2 = DBSCAN(eps=0.2, min_samples=5)
dbscan2.fit(X)
dbscan2.labels_[:20]
array([0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1])
원하는 결과가 나온듯 하다. 위 훈련 결과를 그림으로 나타내면 다음과 같다.

dbscan의 특징에서 설명한것과 같이 이 알고리즘은 새로운 샘플에 대해 예측할 수 없다. dbscan으로 만든 모델을 통한 새로운 샘플에 대한 예측은 지도학습 기반의 새로운 분류기를 만들어 수행한다. 과정은 다음과 같다.
(1) dbscan의 결과 데이터셋의 각 샘플에 할당된 클러스터를 label로 지정한다.
(2) 필요한 분류기(classifier)를 선택 후 훈련시킨다.
(3) 예측이 필요한 샘플을 새로 만든 분류기의 predict 매서드에 전달한다.
dbscan의 결과를 KNeighborClassifier를 통해 훈련시켜보자.
from sklearn.neighbors import KNeighborsClassifier
dbscan = dbscan2
knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])
X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.1], [2, 1]])
knn.predict(X_new)
array([1, 0, 1, 0])
훈련데이터의 특성인 dbscan.components_은 dbscan에서 core point들의 집합이다. 훈련데이터의 라벨인 dbscan.labels_[dbscan.core_sample_indices_]은 core point들의 라벨이다. 새 분류기에 대한 훈련으로 전체 데이터를 이용할 것인지 코어 데이터를 이용할 것인지는 분석가의 판단에 달려있다.
다음 매서드를 통해 각 클러스터에 대한 확률도 추정할 수 있다.
knn.predict_proba(X_new)
array([[0.18, 0.82],
[1. , 0. ],
[0.12, 0.88],
[1. , 0. ]])
Reference
(1) 핸즈온 머신러닝 2판 (오렐리앙 제롱 지음. 박해선 옮김)
(2) 핸즈온 머신러닝 챕터9 주피터 노트북(박해선)


Leave a comment